Thiele / Small-Parameter, ein Leitfaden für die mysteriöse Welt der Lautsprecherspezifikationen
Die Thiele / Small-Parameter sind als wertvolle Spezifikationen bekannt, welche die Niederfrequenzleistung von Lautsprechertreibern bestimmen. Die Parameter sind nach zwei australischen Lautsprecheringenieuren benannt: Richard H. Small und A. Neville Thiele. Nachdem Thiele die Forschungsarbeit "Loudspeakers in Vented Boxes" und Small "Direct-Radiator Loudspeaker System Analysis", "Closed-Box Loudspeaker Systems" und "Vented-Box Loudspeaker Systems" vorgestellt hatte, mussten die Lautsprecheringenieure nicht mehr auf ihr Bauchgefühl verlassen, sondern konnten sich an den vorgestellten Parametern orientieren.
Die Forschungsarbeit präsentierte eine Reihe von Parametern, um das elektroakustische Verhalten von Lautsprechern in geschlossenen und belüfteten Gehäusen vorherzusagen. Thiele und Small schlugen vor, dass alle Lautsprecherhersteller diese Parameter für ihre Produkte zur Verfügung stellen sollten. Glücklicherweise haben es die meisten Hersteller getan, wodurch jetzt jeder diese Parameter verwenden kann, um einen Teil des akustischen Verhaltens seines DIY-Audiodesigns vorherzusagen. Thiele bezeichnet die Lautsprechertechnik vor der Veröffentlichung ihrer Forschungsarbeiten als schwarze Kunst. Mit all den Symbolen und Zahlen mag es immer noch wie eine Art Magie aussehen. Dieser Artikel soll Ihnen dabei helfen, das Rätsel um die T / S-Parameter zu lösen.
Es ist wichtig zu wissen, dass das System auf der Theorie der Schaltungsanalyse basiert. Alle Parameter beziehen sich auf Ersatzschaltbildkomponenten wie Kondensatoren, Induktivitäten und Widerstände. Daher sind die meisten Parameter eng miteinander verbunden und durch mathematische Gleichungen miteinander verflochten. Die für das Ersatzschaltbildmodell verwendeten physikalischen Parameter werden als elektromechanische Parameter bezeichnet. Sie werden auch als Grundparameter bezeichnet, da sie die Kleinsignalleistung steuern. Die praktischsten Parameter sind die Kleinsignalparameter. Sie werden so genannt, weil ein kleines Signal zur Messung der Impedanz der Schwingspulen verwendet wird. Die Impedanzkurve kann erstellt werden, und das resultierende Diagramm ähnelt Abbildung 3. Die Daten aus der Kurve können zur Bestimmung der Kleinsignalparameter verwendet werden. Die Dayton Audio Dats V3 und Audiomatica Clio Pocket 2.0 wurden speziell entwickelt, um diese Daten schnell und einfach zu erfassen. Die zur Berechnung der maximalen Leistung verwendeten Parameter sind die Großsignalparameter.
Dieser Artikel wird nicht zu tief in die grundlegenden Parameter, die Mathematik oder die Theorie der Schaltungsanalyse eintauchen. Aber bitte lassen Sie sich nicht abschrecken, wenn einige Gleichungen auftauchen. Diese Gleichungen zeigen nur auf kompakte Weise wesentliche Beziehungen zwischen den Parametern.
Elektromechanische Parameter | Kleinsignalparameter | Großsignalparameter |
| Sd – Membranfläche | Fs - Resonanzfrequenz | Xmax - Maximale Auslenkung |
| Mms – Bewegliche Masse | Qes - Elektrische Güte | Pe - Belastbarkeit |
| Cms – Nachgiebigkeit der Aufhängung | Qms – Mechanische Güte | Vd – Verschiebevolumen |
| Rms – Mechanischer Widerstand | Qts - Gesamtgüte | |
| Re – Gleichstromwiderstand | Vas - Äquivalentvolumen | |
| Bl – Kraftfaktor |
Die Parameter finden (und vergleichen) Sie unter den Lautsprecherspezifikationen auf unseren Produktseiten. Es gibt jedoch einige "versteckte Juwelen", die nicht von allen Herstellern aufgeführt werden. Diese Parameter erfüllen beim Entwerfen eines Gehäuses keinen direkten Zweck. Einige davon sind jedoch wichtig und werden in diesem Artikel behandelt, um die Beziehungen untereinander zu erläutern.
Die großen drei
Drei wichtige Parameter heben sich von den anderen ab, da sie die Grundlage für die Berechnung der anderen bilden. Zwei dieser wesentlichen Elemente werden üblicherweise vom Hersteller veröffentlicht: die Resonanzfrequenz (Fs) und der Gleichstromwiderstand (Re). Der dritte bemerkenswerte Parameter ist die maximale Impedanz (Zmax). Alle drei sind irgendwo auf der Impedanz Kurve sichtbar. Die Resonanzfrequenz und die maximale Impedanz stellen den gleichen Punkt auf der Impedanz Kurve dar. Folglich ist die Impedanz maximal, wenn der Lautsprecher seine Resonanzfrequenz erreicht. Der Gleichstromwiderstand ist im Impedanz Diagramm sichtbar, in welchem die Frequenz Null ist, da die Gleichspannung eine Frequenz von Null hat. Mit einigen Berechnungen, die auf diese Werte angewendet werden, können andere T / S-Parameter abgeleitet werden.
Resonanzfrequenz (Fs): Dies ist die Frequenz, bei welcher der Lautsprecher mitschwingt. Die beweglichen Teile (Korb, Sicke, Spinne und Schwingspule) haben eine bestimmte Masse und Nachgiebigkeit (Umkehrung der Steifheit). Diese Kombination wird oft als Masse vereinfacht, die an einer Feder befestigt ist.
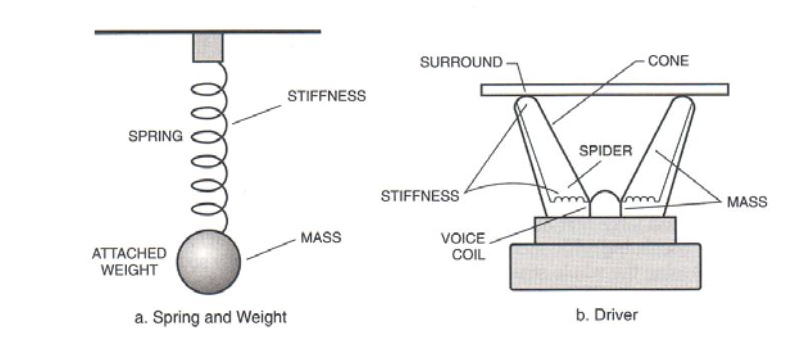
Abbildung 2. Die Analogie zwischen Feder und Lautsprechertreiber. Abbildung 2.3 [Detail] von Alden, R. (2004); Lautsprechergebäude 201: mit 11 vollständig gestalteten Lautsprechersystemen, einschließlich eines 5.1-Heimkinosystems, S.20.
Wenn die Masse in Bewegung gesetzt wird, wird sich die Feder dehnen. Eine Dehnungsfeder "speichert" Energie und möchte in ihren ursprünglichen Zustand zurückkehren. Ab einem bestimmten Punkt reicht die Bewegungsenergie der Masse nicht mehr aus, um die Saite zu dehnen. Die gespeicherte Energie in der gespannten Feder ist stark genug, um die Masse in die entgegengesetzte Richtung zu ziehen. Die sich bewegende Masse überspringt den Gleichgewichts- / Ruhezustand der Feder und bewirkt, dass sich die Feder zusammendrückt. Außerdem speichert die Kompression Energie und bewirkt schließlich, dass sich die Masse wieder in die entgegengesetzte Richtung bewegt. Diese Hin-und-Her-Bewegung, die immer wieder stattfindet, wirkt als ein Resonator. Die Resonanzfrequenz ist die Frequenz, bei der sich die Masse auf der Feder am freiesten hin und her bewegt.
Gleichstromwiderstand (Re): Dies ist der Gleichstromwiderstand der Schwingspule eines Lautsprechers. Üblicherweise wird Re gemessen, um eine Schätzung einer unbekannten (nominalen) Impedanz zu erhalten. Neben groben Schätzungen ist Re nützlich, um Qms zu berechnen.
Maximale Impedanz (Zmax): Achtung, dies ist ein verstecktes Juwel: nicht direkt für die Gehäuseberechnung erforderlich, aber dennoch wertvoll! Wenn Sie die geometrischen Mittelwerte für Re und Zmax (√ (Re x Zmax) = Rc) verwenden, können Sie die Seitenfrequenzen nahe der Resonanzfrequenz bestimmen. Diese Seitenfrequenzen werden bei der Berechnung des Qualitätsfaktors verwendet.
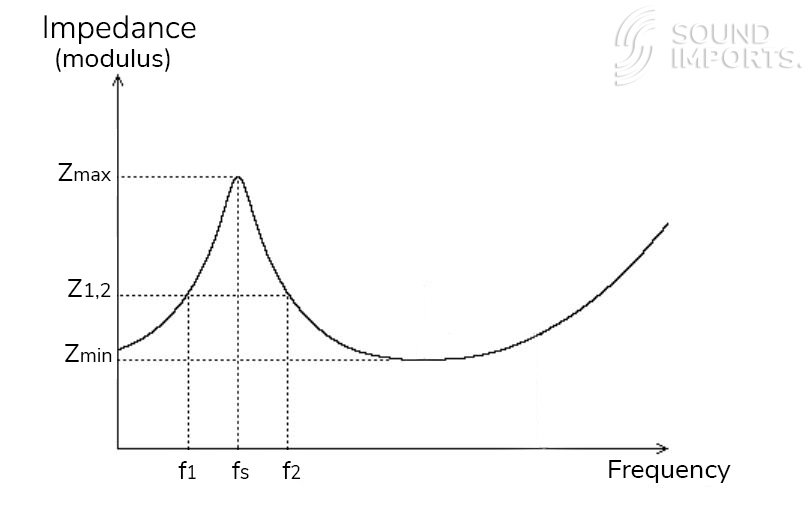
Abbildung 3. SB Acoustics, Technical note "Measuring Thiele/Small parameters", p.2; [Available for download]
Alles über Qualität (Q)
Natürlich ist Qualität etwas, das Sie beim Entwerfen eines Lautsprechers anstreben. Neben dem Entwurf eines anständigen Systems hat Qualität eine weitere Anwendung in der Lautsprechertechnik. Dies wird hauptsächlich als Buchstabe Q bezeichnet. Q ist die Abkürzung für den Qualitätsfaktor. Dieses Maß ohne Einheit ist die Umkehrung der Dämpfung; Ein höheres Q bedeutet ein weniger gedämpftes System. Es zeigt praktisch an, wie lange ein Resonator in Resonanz bleibt. Zurück zur Analogie "Masse an einer Feder befestigt": Q gibt an, wie oft sich die Masse hin und her bewegt, wobei jede Bewegung kürzer ist, bis sich das System wieder in seiner Ruheposition befindet. Der Qualitätsfaktor zeigt sich in folgenden Kleinsignalparametern:
Qms = Die mechanische Güte. Dies zeigt, in welchem Maße das mechanische System bei der Resonanzfrequenz gedämpft wird. Das mechanische System besteht aus beweglicher Masse (gespeicherte Energie) und Aufhängungsverlusten (Verlustleistung).
Qes = Die elektrische Güte. Ein Lautsprecher ist so eingestellt, dass er sich durch ein in die Schwingspule getriebenes Signal bewegt. Da das Signal eine Bewegung erzeugen kann, kann die Bewegung ein (Gegen-) Signal erzeugen. Dies wird als Gegen-EMK bezeichnet und wirkt dem Stromfluss durch die Schwingspule nahe der Resonanzfrequenz entgegen. Die Impedanz wird erhöht und die Bewegung des Kegels wird entgegengesetzt.
Qts = Der kombinierte Wert von Qms und Qes. Um Qts zu berechnen, benötigen Sie das Produkt über der Summe (Qes x Qms / Qes + Qms). Dies kann auch als die gespeicherte Energie geteilt durch die dissipierte Energie beschrieben werden.
Das Luftvolumen mit äquivalenter Übereinstimmung der Aufhängung (Vas)
Der Vas-Parameter beschreibt das Luftvolumen, das die gleiche Nachgiebigkeit (Umkehrung der Steifheit) aufweist wie die Aufhängung des Treibers. Beachten Sie, dass dies keine Empfehlung für das Gehäusevolumen ist. Der Vas-Parameter beschreibt eine Eigenschaft der Aufhängung des Treibers. Obwohl die Luft überall um uns herum ist, hinterlässt sie tendenziell keinen Eindruck. Daher ist es schwierig, ihre physikalischen Eigenschaften zu erfassen. Die Nachgiebigkeit von Luft ist zu spüren, wenn sie eingeschlossen ist. Wenn Sie den Ballon mit Ihren Händen komprimieren, wirkt die Luft im Inneren als Federung und federt zurück. Dies waren die Kleinsignalparameter, außer dass Re ein elektromechanischer Parameter ist. Als nächstes finden Sie eine Übersicht über andere elektromechanische Parameter.
Bewegliche Masse (Mms): Die bewegte Masse ist die Masse aller Teile, die während einer Exkursion in Bewegung sind. Dies schließt auch die „Luftlast“ ein; Die Masse der Luft, gegen die die Oberfläche drückt. Die bewegte Masse ist ein wichtiger Teil der Resonanzfrequenz, aber auch der Q-Faktoren.
Nachgiebigkeit der Aufhängung (Cms): Dies ist die mechanische Konformität der Treiberaufhängung. Nachgiebigkeit ist das Gegenteil von Steifheit. Es spielt auch eine wichtige Rolle bei der Resonanzfrequenz, den Q-Faktoren und auch bei Vas.
Mechanischer Widerstand der Treiberaufhängungsverluste (Rms): Die Aufhängung speichert Energie (wie bei der im Resonanzfrequenzabschnitt dargestellten Analogie "Masse an einer Feder"), die Aufhängung weist auch "Verluste" auf. Ein Teil der in der Feder gespeicherten Energie geht durch dissipative Komponenten wie Reibung verloren. Diese Verluste wirken der Bewegung der Membrane entgegen.
Membranfläche (Sd): Dies ist der Teil, der die Bewegung von der Schwingspule in die Luft überträgt. Da sich ungefähr die Hälfte der Membranaufhängung mit der Membran bewegt, ist Sd etwas größer als die Membranfläche selbst.
Weitere versteckte Juwelen (akustische Komponenten)
Dies mag etwas schwer zu verstehen sein, aber die oben beschriebenen Parameter für die sich bewegende Masse, die Nachgiebigkeit der Aufhängung und den mechanischen Widerstand hängen mit ihren akustischen Äquivalenten über den Oberflächenparameter zusammen. Die folgenden Gleichungen zeigen, dass die Berechnungen für die akustischen Komponenten nicht so kompliziert sind:
Cms x Sd² = Cas = Akustische Nachgiebigkeit der Aufhängung
Mms/Sd² = Mas = Schallmasse beweglicher Teile
Rms/Sd² =Ras = Schallwiderstand der Treiberaufhängung
Einfach ausgedrückt sind die akustischen Komponenten die Verbindung zwischen den Grundparametern und den Kleinsignalparametern. Zum Beispiel ist der Kehrwert der quadratischen Resonanzfrequenz (als Winkelfrequenz ω) durch die akustische Nachgiebigkeit der Zeit "akustische Masse“ (Cas ×Mas = 1/ωs²) gegeben.
Force factor (Bl): Dieser Parameter besteht aus B x L. "B" bezieht sich auf die Flussdichte (Stärke des Magnetfelds) und "L" auf die Länge der Schwingspule. Dieser Parameter ist wichtig, da er die Kraft beschreibt, die vom Magneten erzeugt wird, wenn ein Signal durch die Spule fließt. Bl bezeichnet den Wert von Qes, da der quadratische Wert der Nenner im Qes-Ausdruck ist (ωsReMasSd²/ Bl²).
Großsignalparameter: Die Großsignalparameter beziehen sich auf das größte Signal, das ein Lautsprecher verarbeiten kann.
Pe = Gibt an, wie viel Leistung der Lautsprecher verarbeiten kann. Die Belastbarkeit weist auf eine thermische Grenze hin und ist durch die Wärmemenge begrenzt, die die Schwingspule (und die umgebenden Strukturen) abgeben können. Wenn der Grenzwert erreicht ist, erwärmt sich die Schwingspule zu stark und wird eventuell beschädigt.
Xmax = Maximale lineare Auslenkung. Xmax gibt an, welche Entfernung die Schwingspule (auf eine Weise) zurücklegen kann, während sie weiterhin linear bleibt.
Vd = maximales Verschiebevolumen oder maximale Volumenverschiebung, üblicherweise ausgedrückt in cm³. Das maximale Verschiebevolumen wird mit Xmax × Sd berechnet. Vd und es ist die maximale Luftmenge, die der Lautsprecher in Bewegung setzt, während er immer noch linear bleibt. Das Verschiebevolumen wird zur Berechnung der Schallleistung verwendet.
Wir hoffen, dass dieser Artikel Licht ins Dunkle der T / S-Parameter brachte und Sie diese bei der Gestaltung Ihres nächsten DIY-Audioprojekts verwenden können.
Literaturhinweise
- Alden, R., "Speaker Building 201: with 11 Completely Designed Speaker Systems including a 5.1 Home Theater System", Audio Amateur Press (2004).
- Gomez-Meda, R., "Measurement of the Thiele-Small parameters for a given loudspeaker, without using a box. In Audio Engineering Society Convention 91; Audio Engineering Society (October, 1991).
- Small, R.H., "Closed-Box Loudspeaker Systems", J. Audio Eng. Soc., vol. 20, pp. 798–808 (Dec. 1972); vol. 21, pp. 11–18 (Jan./Feb. 1973).
- Small, R.H., "Direct-Radiator Loudspeaker System Analysis", J. Audio Eng. Soc., vol. 20, pp. 383–395 (June 1972).
- Small, R.H., "Vented-Box Loudspeaker Systems", J. Audio Eng. Soc., vol. 21, pp. 363–372 (June 1973); pp. 438–444 (July/Aug. 1973); pp. 549–554 (Sept. 1973); pp. 635–639 (Oct. 1973).
- Thiele, A.N., "Loudspeakers in Vented Boxes," Proceedings of the Institute of Radio Engineers, Australia, 22(8), pp. 487-508. Reprinted in Journal of the Audio Engineering Society, 1971, 19 (5 & 6), pp. 382-392 & 471-483. Reprinted in R.E. Cooke (ed.) Loudspeakers, An Anthology, Vol. 1 - Vol. 25 (1953-1977), Audio Engineering Society, New York, 1978, pp. 181-204. Reprinted in Vented Loudspeakers - An Anthology, Institute of Radio and Electronics Engineers (1961).
- Thiele, A.N., "Loudspeakers in Vented Boxes, Parts I and II", J. Audio Eng. Soc., vol. 19, pp. 382–392 (May 1971); pp. 471–483 (June 1971).

 Home-Audio
Home-Audio  Audio Komponenten
Audio Komponenten  Frequenzweichen-Bauteile
Frequenzweichen-Bauteile  Testen & Messen
Testen & Messen  Bausätze
Bausätze  Zubehör
Zubehör  Neue Produkte
Neue Produkte  SALE
SALE  Lautsprecher
Lautsprecher Verstärker
Verstärker  DAC Wandler
DAC Wandler DSP Module
DSP Module Streamer
Streamer Plattenspieler
Plattenspieler Tieftöner
Tieftöner Hochtöner
Hochtöner Exciter
Exciter Bass Shakers
Bass Shakers Einbauverstärker
Einbauverstärker Verstärkermodule
Verstärkermodule Montierte Frequenzweichen
Montierte Frequenzweichen Leiterplatten
Leiterplatten Kondensatoren
Kondensatoren Widerstände
Widerstände Spulen
Spulen Circuit Breakers
Circuit Breakers Schraubklemmen
Schraubklemmen Akustikmessungen
Akustikmessungen Elektrische Messungen
Elektrische Messungen Schallpegelmesser
Schallpegelmesser Verstärker Bausätze
Verstärker Bausätze Komponentenpakete
Komponentenpakete Lautsprecher-Bausätze
Lautsprecher-Bausätze Subwoofer Bausätze
Subwoofer Bausätze Bluetooth Lautsprecher Bausätze
Bluetooth Lautsprecher Bausätze DIY-Elektronik-Bausätze
DIY-Elektronik-Bausätze Polklemmen
Polklemmen Gehäusebeschläge
Gehäusebeschläge Kabel
Kabel Stecker
Stecker Lautsprecher Gehäuse
Lautsprecher Gehäuse Elektromechanik
Elektromechanik Netzteile
Netzteile Lautsprecher Reparatur
Lautsprecher Reparatur Werkstatt Werkzeuge
Werkstatt Werkzeuge Verstärkerzubehör
Verstärkerzubehör Ständer & Halterungen
Ständer & Halterungen Geschenkgutschein
Geschenkgutschein Bücher
Bücher Neue Produkte
Neue Produkte Angebote unter 100 €
Angebote unter 100 € Angebote Ab 100 €
Angebote Ab 100 € 









 Lautsprecher
Lautsprecher Verstärker
Verstärker  DAC Wandler
DAC Wandler DSP Module
DSP Module Streamer
Streamer Plattenspieler
Plattenspieler Tieftöner
Tieftöner Hochtöner
Hochtöner Exciter
Exciter Bass Shakers
Bass Shakers Einbauverstärker
Einbauverstärker Verstärkermodule
Verstärkermodule Montierte Frequenzweichen
Montierte Frequenzweichen Leiterplatten
Leiterplatten Kondensatoren
Kondensatoren Widerstände
Widerstände Spulen
Spulen Circuit Breakers
Circuit Breakers Schraubklemmen
Schraubklemmen Akustikmessungen
Akustikmessungen Elektrische Messungen
Elektrische Messungen Schallpegelmesser
Schallpegelmesser Verstärker Bausätze
Verstärker Bausätze Komponentenpakete
Komponentenpakete Lautsprecher-Bausätze
Lautsprecher-Bausätze Subwoofer Bausätze
Subwoofer Bausätze Bluetooth Lautsprecher Bausätze
Bluetooth Lautsprecher Bausätze DIY-Elektronik-Bausätze
DIY-Elektronik-Bausätze Polklemmen
Polklemmen Gehäusebeschläge
Gehäusebeschläge Kabel
Kabel Stecker
Stecker Lautsprecher Gehäuse
Lautsprecher Gehäuse Elektromechanik
Elektromechanik Netzteile
Netzteile Lautsprecher Reparatur
Lautsprecher Reparatur Werkstatt Werkzeuge
Werkstatt Werkzeuge Verstärkerzubehör
Verstärkerzubehör Ständer & Halterungen
Ständer & Halterungen Geschenkgutschein
Geschenkgutschein Bücher
Bücher Neue Produkte
Neue Produkte Angebote unter 100 €
Angebote unter 100 € Angebote Ab 100 €
Angebote Ab 100 €  Dayton Audio Exciters
Dayton Audio Exciters




