Parametri Thiele/Small, una guida al misterioso mondo delle specifiche dei diffusori acustici
I parametri Thiele/Small sono specifiche preziose che determinano le prestazioni in bassa frequenza dei driver per altoparlanti. Questi parametri prendono il nome da due ingegneri australiani specializzati in progettazione di altoparlanti: Richard H. Small e A. Neville Thiele.
Dopo che Thiele presentò il suo celebre articolo "Loudspeakers in Vented Boxes", seguito dagli studi di Small con "Direct-Radiator Loudspeaker System Analysis", "Closed-Box Loudspeaker Systems" e "Vented-Box Loudspeaker Systems", i progettisti di altoparlanti non dovevano più affidarsi al metodo del tentativo e dell’errore. Gli articoli introdussero un insieme di parametri utili per prevedere il comportamento elettroacustico degli altoparlanti in sistemi sigillati e reflex. Thiele e Small proposero che tutti i produttori di altoparlanti rendessero pubblici questi parametri per ogni prodotto. Fortunatamente, la maggior parte dei produttori ha seguito questa raccomandazione, e oggi chiunque può utilizzare tali parametri per prevedere parte del comportamento acustico del proprio progetto audio DIY. Thiele definì l’ingegneria degli altoparlanti, prima della pubblicazione del loro lavoro, come una sorta di “arte nera”. E, con tutti i simboli e numeri coinvolti, può ancora sembrare un po’ magico. Questo articolo è pensato per aiutarti a svelare il mistero dietro i parametri T/S.
È importante sapere che il sistema si basa sulla teoria dell’analisi circuitale. Tutti i parametri sono collegati a componenti equivalenti di un circuito elettrico, come condensatori, induttori e resistori. Per questo motivo, la maggior parte dei parametri è strettamente correlata e interconnessa tramite equazioni matematiche. I parametri fisici utilizzati nel modello di circuito elettrico equivalente sono chiamati parametri elettromeccanici, noti anche come parametri fondamentali, poiché determinano le prestazioni in regime di piccolo segnale. I parametri più pratici per la progettazione sono infatti i parametri di piccolo segnale (small-signal parameters), così chiamati perché vengono misurati applicando un segnale di bassa ampiezza per determinare l’impedenza della bobina mobile. L’impedenza viene quindi tracciata su un grafico simile a quello della Figura 2. I dati della curva vengono poi utilizzati per calcolare i parametri di piccolo segnale. Strumenti come il Dayton Audio Dats V3 e l’Audiomatica Clio Pocket 2.0 sono specificamente progettati per acquisire questi dati in modo rapido e semplice. I parametri di grande segnale (large-signal parameters) vengono invece utilizzati per calcolare le prestazioni massime del driver.
Questo articolo non approfondirà nel dettaglio i parametri fondamentali, la matematica o la teoria dei circuiti. Tuttavia, non lasciarti intimorire se dovessero apparire alcune formule: queste serviranno solo a mostrare le relazioni essenziali tra i parametri in modo compatto.
| Parametri elettromeccanici | Parametri di piccolo segnale (Small-signal) | Parametri di grande segnale (Large-signal) |
| Sd – Superficie del diaframma | Fs - Frequenza di risonanza | Xmax - Escursione massima lineare |
| Mms – Massa mobile | Qes - Fattore di merito elettrico | Pe - Potenza nominale |
| Cms – Cedevolezza della sospensione | Qms – Fattore di merito meccanico | Vd – Spostamento volumetrico |
| Rms – Resistenza meccanica | Qts - Fattore di merito totale (combinato) | |
| Re – Resistenza in continua (DC) | ||
| Bl – Fattore di forza |
I parametri possono essere trovati (e confrontati) nelle specifiche tecniche degli altoparlanti presenti nelle nostre pagine prodotto. Tuttavia, ci sono alcune "perle nascoste" che non vengono riportate da tutti i produttori. Questi parametri non hanno un ruolo diretto nella progettazione del cabinet, ma alcuni di essi sono comunque importanti e riceveranno l’attenzione che meritano in questo articolo, al fine di spiegare le relazioni che li legano agli altri parametri.
I tre fondamentali
Tre parametri importanti si distinguono dagli altri perché costituiscono le basi per calcolare tutti gli altri. Due di questi sono normalmente forniti dal produttore: la frequenza di risonanza (Fs) e la resistenza in continua (Re). Il terzo parametro fondamentale è l’impedenza massima (Zmax). Tutti e tre sono visibili sul grafico dell’impedenza. La frequenza di risonanza e l’impedenza massima corrispondono allo stesso punto della curva: infatti, l’impedenza è massima quando il diffusore raggiunge la sua frequenza di risonanza. La resistenza in continua (Re) si può osservare nella parte iniziale del grafico, dove la frequenza è pari a zero, poiché una tensione continua ha una frequenza pari a zero. Applicando alcuni calcoli a questi valori, è possibile derivare gli altri parametri T/S.
Frequenza di risonanza (Fs): Questa è la frequenza alla quale l'altoparlante entra in risonanza. Le parti mobili del driver (cono, sospensione, spider e bobina mobile) hanno una certa massa e una certa cedevolezza (ovvero l’inverso della rigidità). Questa combinazione viene spesso semplificata come una massa collegata a una molla.
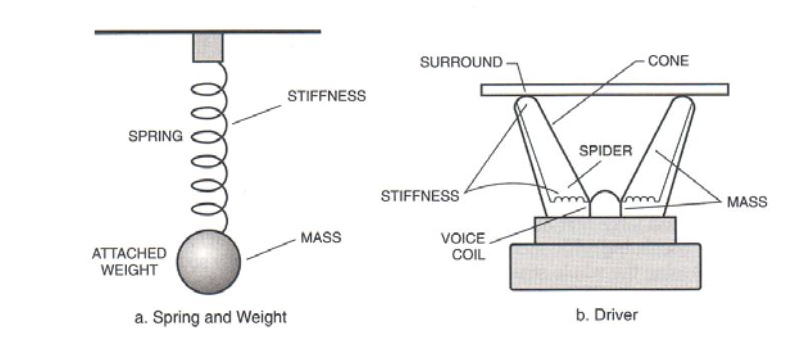
Fig. 1 – L’analogia tra una molla e un driver per altoparlante. Figura 2.3 [dettaglio], tratta da: Alden, R. (2004); Speaker Building 201: with 11 Completely Designed Speaker Systems including a 5.1 Home Theater System, p.20.
Quando la massa viene messa in movimento, la molla si allunga. Una molla allungata immagazzina energia e tende a tornare al suo stato originale. A un certo punto, l’energia cinetica della massa non è più sufficiente per allungare ulteriormente la molla. L’energia accumulata nella molla, ora allungata, è abbastanza forte da tirare la massa nella direzione opposta. La massa in movimento supera lo stato di equilibrio (o di riposo) della molla, provocando la compressione della molla stessa. Anche la compressione immagazzina energia, che a sua volta spinge la massa di nuovo nella direzione opposta. Questo movimento avanti e indietro che si ripete nel tempo è un comportamento di tipo risonante. La frequenza di risonanza è quella in cui la massa si muove avanti e indietro con la massima libertà, sospesa sulla molla.
Resistenza in continua (Re): È la resistenza DC della bobina mobile di un altoparlante. Normalmente, Re viene misurata per stimare l’impedenza nominale di un altoparlante sconosciuto. Oltre a fornire una stima approssimativa, Re è utile per il calcolo del Qms (fattore di merito meccanico).
Impedenza massima (Zmax): Attenzione: questo è uno dei parametri “nascosti”! Non è direttamente necessario per il calcolo del volume del cabinet, ma è comunque molto utile.Utilizzando la media geometrica tra Re e Zmax: √(Re × Zmax) = Rc si può determinare la frequenza ai lati della frequenza di risonanza. Queste frequenze laterali vengono utilizzate nel calcolo del fattore di merito (Q).
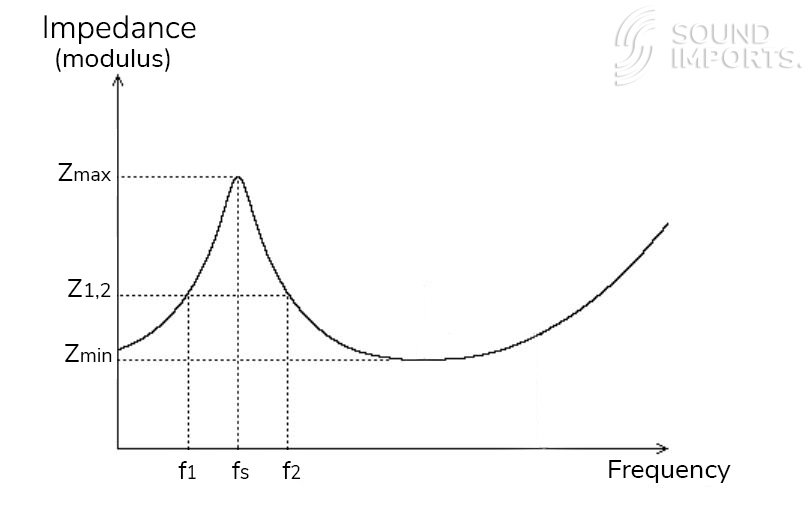
Fig. 2 – SB Acoustics, Nota tecnica "Measuring Thiele/Small parameters", p.2; [Disponibile per il download]
Tutto sulla qualità (Q)
Naturalmente, la qualità è un obiettivo fondamentale nella progettazione di un diffusore acustico. Ma oltre a indicare la bontà del progetto nel suo insieme, in ambito ingegneristico la “Qualità” ha un significato specifico e viene solitamente indicata con la lettera Q. Q è l’abbreviazione di “fattore di qualità” (Quality Factor). Si tratta di una misura senza unità di misura, ed è l’inverso dello smorzamento: un valore Q elevato indica un sistema meno smorzato. In pratica, Q indica quanto a lungo un sistema risonante continua a vibrare. Ritornando all’analogia della massa collegata a una molla, il valore di Q indica quante volte la massa oscilla avanti e indietro, con ogni movimento progressivamente più breve, fino a quando il sistema ritorna allo stato di riposo. Il fattore di qualità compare nei seguenti parametri di piccolo segnale:
Qms = Fattore di qualità meccanico. Indica quanto è smorzato il sistema meccanico alla frequenza di risonanza. Il sistema meccanico è costituito dalla massa mobile (energia immagazzinata) e dalle perdite nella sospensione (energia dissipata).
Qes = Fattore di qualità elettrico. Un altoparlante si muove grazie al segnale applicato alla bobina mobile. Ma quando si muove, il cono genera a sua volta un segnale di ritorno (contro-elettromotrice o back-EMF) che ostacola il flusso di corrente nella bobina vicino alla frequenza di risonanza. Di conseguenza, l’impedenza aumenta e il movimento del cono viene smorzato elettricamente.
Qts = Fattore di qualità totale. È il valore combinato di Qms e Qes. Per calcolare Qts si usa la seguente formula: Qts = (Qes × Qms) / (Qes + Qms). Questa relazione può anche essere interpretata come: energia immagazzinata divisa per energia dissipata.
Il volume d’aria con cedevolezza equivalente alla sospensione (Vas)
Il parametro Vas descrive il volume d’aria che possiede la stessa cedevolezza (inverso della rigidità) della sospensione del driver. Attenzione: non si tratta di un valore consigliato per il volume del cabinet! Il Vas rappresenta esclusivamente una proprietà della sospensione del driver. Anche se l’aria è ovunque attorno a noi, tende a non lasciare alcuna impressione fisica visibile; per questo motivo, è difficile comprenderne appieno le proprietà. Un esempio pratico si ha comprimendo un palloncino: l’aria al suo interno si comporta proprio come una sospensione elastica. Questi erano i principali parametri di piccolo segnale, fatta eccezione per Re, che è un parametro elettromeccanico. Di seguito trovi una panoramica degli altri parametri elettromeccanici.
Massa mobile (Mms):È la massa di tutte le parti che si muovono durante l’escursione del driver, compreso il cosiddetto “carico d’aria”, cioè la massa dell’aria che viene spinta dalla superficie radiante. La massa mobile incide fortemente sulla frequenza di risonanza e anche sui fattori Q.
Cedevolezza della sospensione (Cms):Indica la cedevolezza meccanica della sospensione del driver. La cedevolezza è l’inverso della rigidità. Anche questo parametro ha un ruolo importante nella frequenza di risonanza, nei fattori Q e nel calcolo del Vas.
Resistenza meccanica delle perdite nella sospensione (Rms): Come già accennato nell’analogia della massa collegata a una molla, la sospensione immagazzina energia, ma presenta anche perdite. Parte dell’energia accumulata viene dissipata a causa di componenti dissipativi, come l’attrito. Queste perdite ostacolano il movimento del cono.
Superficie radiante (Sd):È l’area che trasferisce il movimento dalla bobina mobile all’aria. Poiché circa la metà dell’area circostante si muove insieme al cono, Sd risulta leggermente più grande dell’area del solo cono.
Altre “perle nascoste”: i componenti acustici
Questa parte può risultare un po’ difficile da comprendere, ma i parametri come massa mobile, cedevolezza della sospensione e resistenza meccanica sono collegati ai loro equivalenti acustici proprio attraverso il parametro Sd. Le seguenti equazioni mostrano che i calcoli dei componenti acustici non sono così complessi:
Cms × Sd² = Cas → Cedevolezza acustica della sospensione
Mms / Sd² = Mas → Massa acustica delle parti mobili
Rms / Sd² = Ras → Resistenza acustica della sospensione
In termini semplici, i componenti acustici fanno da ponte tra i parametri fondamentali e i parametri di piccolo segnale. Ad esempio, l’inverso del quadrato della frequenza di risonanza (espressa in radianti/secondo ω) è dato da: Cas × Mas = 1 / ωs²
Fattore di forza (Bl): Questo parametro è il prodotto tra B (densità del flusso magnetico) e L (lunghezza della bobina mobile nel campo magnetico). Bl è importante perché descrive la forza generata dal magnete quando un segnale elettrico attraversa la bobina. Il Bl incide direttamente sul valore del Qes, poiché il suo valore al quadrato è al denominatore nell’equazione del Qes: Qes = (ωs × Re × Mas × Sd²) / Bl²
Parametri di grande segnale: I parametri di grande segnale si riferiscono al comportamento dell’altoparlante quando viene sollecitato al massimo.
Pe = Potenza nominale gestibile. Indica quanta potenza l’altoparlante può sopportare. È legata ai limiti termici del sistema ed è determinata dalla quantità di calore che la bobina mobile (e le strutture circostanti) possono dissipare. Se si supera questo limite, la bobina si surriscalda e può danneggiarsi.
Xmax = Escursione massima lineare. Indica fino a che punto la bobina può spostarsi in una direzione rimanendo nel campo lineare.
Vd = Spostamento volumetrico massimo, solitamente espresso in cm³. È calcolato come: Vd = Xmax × Sd. Rappresenta il massimo volume d’aria che l’altoparlante può mettere in movimento, restando in ambito lineare. Il valore di Vd è utilizzato per calcolare la pressione sonora (SPL) e l’output acustico complessivo.
Speriamo che questo articolo abbia fatto luce sui parametri Thiele/Small e che ora tu possa utilizzarli in modo consapevole nella progettazione del tuo prossimo progetto audio DIY.
Bibliografia
- Alden, R., "Speaker Building 201: with 11 Completely Designed Speaker Systems including a 5.1 Home Theater System", Audio Amateur Press (2004).
- Gomez-Meda, R., "Measurement of the Thiele-Small parameters for a given loudspeaker, without using a box. In Audio Engineering Society Convention 91; Audio Engineering Society (October, 1991).
- Small, R.H., "Closed-Box Loudspeaker Systems", J. Audio Eng. Soc., vol. 20, pp. 798–808 (Dec. 1972); vol. 21, pp. 11–18 (Jan./Feb. 1973).
- Small, R.H., "Direct-Radiator Loudspeaker System Analysis", J. Audio Eng. Soc., vol. 20, pp. 383–395 (June 1972).
- Small, R.H., "Vented-Box Loudspeaker Systems", J. Audio Eng. Soc., vol. 21, pp. 363–372 (June 1973); pp. 438–444 (July/Aug. 1973); pp. 549–554 (Sept. 1973); pp. 635–639 (Oct. 1973).
- Thiele, A.N., "Loudspeakers in Vented Boxes," Proceedings of the Institute of Radio Engineers, Australia, 22(8), pp. 487-508. Reprinted in Journal of the Audio Engineering Society, 1971, 19 (5 & 6), pp. 382-392 & 471-483. Reprinted in R.E. Cooke (ed.) Loudspeakers, An Anthology, Vol. 1 - Vol. 25 (1953-1977), Audio Engineering Society, New York, 1978, pp. 181-204. Reprinted in Vented Loudspeakers - An Anthology, Institute of Radio and Electronics Engineers (1961).
- Thiele, A.N., "Loudspeakers in Vented Boxes, Parts I and II", J. Audio Eng. Soc., vol. 19, pp. 382–392 (May 1971); pp. 471–483 (June 1971).

 Audio domestico
Audio domestico  Componenti audio
Componenti audio  Componenti crossover
Componenti crossover  Test e misurazioni
Test e misurazioni  Kit fai da te
Kit fai da te  Accessori
Accessori  Nuovi prodotti
Nuovi prodotti  Diffusori
Diffusori Amplificatori
Amplificatori Convertitori Digitali Analogici
Convertitori Digitali Analogici Moduli DSP
Moduli DSP Giradischi
Giradischi Streamer
Streamer Woofers
Woofers Tweeters
Tweeters Eccitatori
Eccitatori Bass shakers
Bass shakers Amplificatori a piastra
Amplificatori a piastra Modulo amplificatore
Modulo amplificatore Computer Scheda Singola
Computer Scheda Singola Crossover assemblati
Crossover assemblati Basette crossover
Basette crossover Condensatori
Condensatori Resistori
Resistori Induttori
Induttori Interruttori automatici
Interruttori automatici Dispositivi per crossover
Dispositivi per crossover Terminali a vite
Terminali a vite Misurazioni acustiche
Misurazioni acustiche Misurazioni elettriche
Misurazioni elettriche Fonometri
Fonometri Kit amplificatori fai da te
Kit amplificatori fai da te Kit autocostruzione
Kit autocostruzione Kit altoparlanti fai da te
Kit altoparlanti fai da te Kit subwoofer fai da te
Kit subwoofer fai da te Kit altoparlanti bluetooth fai da te
Kit altoparlanti bluetooth fai da te Kit di elettronica fai da te
Kit di elettronica fai da te Morsetti
Morsetti Cabinet altoparlanti
Cabinet altoparlanti Cavi
Cavi Connettori
Connettori Box per altoparlanti
Box per altoparlanti Elettromeccanica
Elettromeccanica  Alimentatori
Alimentatori Riparazione diffusori
Riparazione diffusori Attrezzatura e strumentazione
Attrezzatura e strumentazione Accessori per amplificatori
Accessori per amplificatori Supporti e staffe
Supporti e staffe Buono regalo
Buono regalo Letteratura
Letteratura Nuovi prodotti
Nuovi prodotti









 Diffusori
Diffusori Amplificatori
Amplificatori Convertitori Digitali Analogici
Convertitori Digitali Analogici Moduli DSP
Moduli DSP Giradischi
Giradischi Streamer
Streamer Woofers
Woofers Tweeters
Tweeters Eccitatori
Eccitatori Bass shakers
Bass shakers Amplificatori a piastra
Amplificatori a piastra Modulo amplificatore
Modulo amplificatore Computer Scheda Singola
Computer Scheda Singola Crossover assemblati
Crossover assemblati Basette crossover
Basette crossover Condensatori
Condensatori Resistori
Resistori Induttori
Induttori Interruttori automatici
Interruttori automatici Dispositivi per crossover
Dispositivi per crossover Terminali a vite
Terminali a vite Misurazioni acustiche
Misurazioni acustiche Misurazioni elettriche
Misurazioni elettriche Fonometri
Fonometri Kit amplificatori fai da te
Kit amplificatori fai da te Kit autocostruzione
Kit autocostruzione Kit altoparlanti fai da te
Kit altoparlanti fai da te Kit subwoofer fai da te
Kit subwoofer fai da te Kit altoparlanti bluetooth fai da te
Kit altoparlanti bluetooth fai da te Kit di elettronica fai da te
Kit di elettronica fai da te Morsetti
Morsetti Cabinet altoparlanti
Cabinet altoparlanti Cavi
Cavi Connettori
Connettori Box per altoparlanti
Box per altoparlanti Elettromeccanica
Elettromeccanica  Alimentatori
Alimentatori Riparazione diffusori
Riparazione diffusori Attrezzatura e strumentazione
Attrezzatura e strumentazione Accessori per amplificatori
Accessori per amplificatori Supporti e staffe
Supporti e staffe Buono regalo
Buono regalo Letteratura
Letteratura Nuovi prodotti
Nuovi prodotti





